前回の5枚、6枚繻子に続き、今回は7枚繻子の世界をご案内します。
7枚繻子は、織物業に携わる人でもほとんど耳にすることはないマイナーな存在です。
人類はそれを見過ごしたままでいて良いのか?
それが今回のテーマです。ちょっとだけ、これまでの復習
繻子織(朱子織)というのは、 このシリーズの第2回 で解説したように、組織図上で組織点「■」が互いに上下左右+斜めで隣接してはならない、各列・行に組織点は必ず一つ、という厳しいルールで作られた織物組織です。
このルールを満たす組織のパターンは、
サイズが5×5の5枚繻子では2種類(正則繻子)、
サイズが6×6の6枚繻子では1種類(不規則繻子)しか存在しません。
このシリーズの前回では、それぞれの繻子織りの種類がどんな対称性を持つかをお伝えしました。
簡単にいうと、
5枚繻子の2つは鏡に映すと互いに入れ替わり、
6枚繻子は1つだけでどんな回転・反転をしても元の形のまま、
という性質です。
7枚繻子のすべてをご紹介
5枚、6枚では合わせて3種類しかなかった繻子織りパターンですが、7枚繻子では一気に10種類に激増します。
下の図に並べたものが、変則繻子も含む7枚繻子の全10パターンです。
これが、この世界にある10種類の7枚繻子。宇宙の果てまで旅をしても、この10個以外には見つからないはずです。
この結果を導き出すために、シケンジョでは繻子組織パターンのあらゆる可能性を抽出するプログラムを作成し、この世に存在する10枚繻子までのすべての変則繻子をこれまでの研究で明らかにしました。
今回のように、変則繻子を含む全ての7枚繻子を網羅的に分類、整理して紹介するのは、もしかしたら世界初の試みかも知れません。
(先行事例をご存じの方がいましたら、お知らせいただけると幸いです)
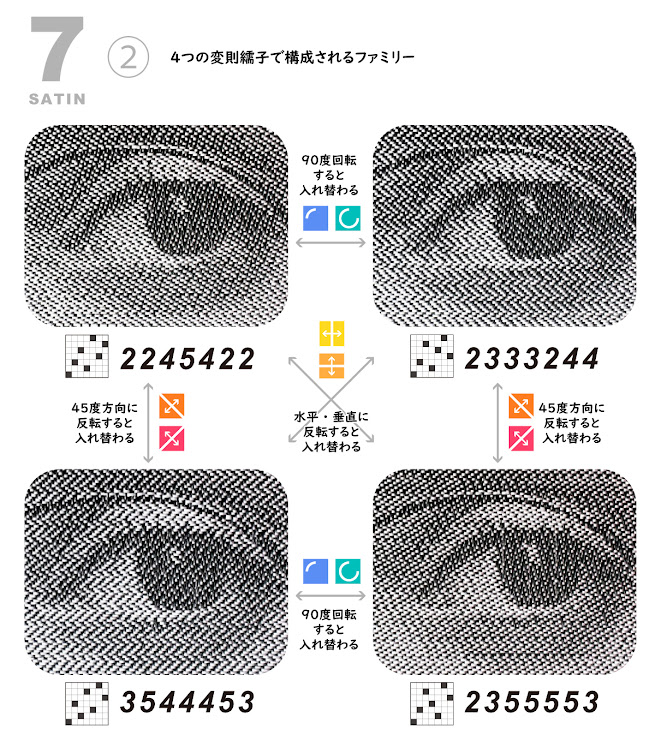
7枚繻子の3つの対称性ファミリー
さらなる解析の結果、これら10種類の7枚繻子は、対称性によって①~③のまとまりに分類できることがわかりました。
①…正則朱子が4つ(2、3、4、5飛び)
②…不規則繻子が4つ(2245422飛び、2333244飛び、3544453飛び、2355553飛び)
③…不規則繻子が2つ(2332353飛び、2454454飛び)
7枚繻子を全部織ってみました
[ 注目ポイント1 ]90度回転すると布の見た目が別物になる
例えば7枚繻子の2飛びと3飛びは、互いに90度回転したもの同士。
[ 注目ポイント3 ]変則繻子は、地紋風のパターンが生まれる
デジタルジャカードで7枚繻子
7枚繻子はなぜ見落とされているのか?
7という数字は、ラッキーセブン、七五三のお祝い、1週間の日数、七つの海、七不思議など、私たちの生活の中ではどちらかというと身近でポジティブな意味で使われる数字です。
しかし最初に書いたように、織物の世界で「7枚繻子」が使われることはほとんどありません。
7枚繻子がほとんど使われない理由を、織機の基本であるドビー織機で考えてみます。
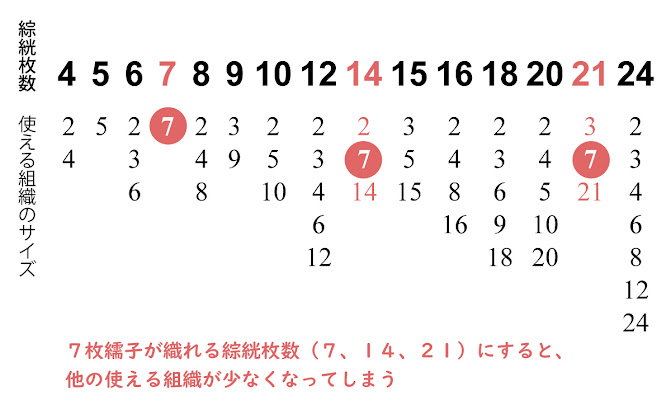
ドビー織機では、タテ糸を動かす機構である綜絖(そうこう)を何枚あるかによって、使える組織のサイズが決まります。それは、綜絖枚数が割り切れるサイズの組織です。
下の図は、様々な綜絖枚数で織れる組織のサイズの一覧をまとめてみました。
これを見ると、7枚繻子が織れる綜絖枚数では、枚数が多いわりに使える種類が少ないことがわかります。
この不便さが、7枚繻子がほとんど使われない大きな理由です。
ドビー織機より自由度の高いジャカード織機であっても、よく使われる最大リピート本数(口数)は960、1344、5760など、7で割り切れないものばかりです。
それでも「7が最適解」というときはあるはず
5でも8でもしっくりこないときに、7を使えば解決したり、あるいは実現したい風合いを表現するのに実は7枚繻子が最適だった、というのは、十分あり得ることだと思います。
もし7枚繻子が最適解というケースがもしあるとしたなら、7枚綜絖、14枚綜絖にトライしたり、ジャカード織機では7枚繻子をリピート境界には使わないですむような柄にするとか、使う方法を試してみるべきではないでしょうか?
なにより、全幅ひと釜で織れる大口ジャカードだったら7枚繻子を使っても何も問題がないはずなのに、それでも7枚繻子が無視されている、というのは非常にもったいないことだと思います。
最後にもう一度、10種類、3ファミリーの7枚繻子をまとめて図で紹介します。
(五十嵐)